0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Bagaimana kita mencari bilangan ke-1000? atau ke-505? Untuk mencari bilangan ke-n dari bilangan fibonacci kita menggunakan rumus binet. Rumus tersebut berkata.
Pertama-tama kita akan membentuk sistem persamaan linier dengan 2 persamaan. Kita tahu bahwa suku ke n+2 fibonacci merupakan penjumlahan dari suku ke n+1 dan suku ke n. Kita peroleh persamaan yang pertama
Jika sistem persamaandiatas diubah ke dalam persamaan matriks, diperoleh
Oya sebelumnya notasi  merupakan suku ke-n dari fibonacci dengan
merupakan suku ke-n dari fibonacci dengan  dan
dan  .
.
Jika kita notasikan Nah sekarang mari kita mulai menghitung

Jadi diperoleh rumus umum
Nah..sekarang pertanyaannya adalah bagaimana menghitung pangkat ke-n dari matriks  secara cepat?
secara cepat?
Cara cepatnya adalah dengan menggunakan 2 matriks spesial 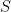 dan
dan 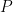 . Matriks
. Matriks 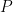 adalah matriks diagonal yang memuat nilai-nilai eigen dari matriks
adalah matriks diagonal yang memuat nilai-nilai eigen dari matriks 
Sedangkan matriks
diperoleh
Berdasarkan persamaan diatas, dengan mudah kita dapet menghitung
Karena
Dengan cara sama kita mendapatkan
Jadi dapat disimpulkan bahwa rumus mencari pangkat ke-n dari matriks
Nah sekarang berapa vektor eigen dan nilai eigen dari
Kita peroleh
dan
Itu berarti kita peroleh
Catetan:
Akhirnya kita dapat
Tidak ada komentar:
Posting Komentar