In your mind

Entah kenapa aku merasa ingin terus membahas skripsiku kemarin. Semoga selalu seperti ini, maksudku ingin terus membaca-baca kembali apa yang aku geluti selama hampir satu tahun itu. Kali ini aku ingin membahas Lemma 2.3.4 yang ada di skripsiku. Selamat membaca ya.
Sebelumnya, didefinisikan terlebih dahulu himpunan $\left(N:M\right)$ yaitu:

$\left(N:M\right)=\left\{ r\in R|rM\subseteq N\right\}$

Eit, jangan sampai lupa ya, bahwa aku “bekerja” dengan ring komutatif R dengan elemen satuan loh ya.
Lemma 2.3.4
Jika M adalah R-modul dan N adalah submodul, maka $\left(N:M\right)$ adalah ideal di ring R.
Bukti :
Diketahui M adalah R-modul. Akan dibuktikan $\left(N:M\right)$ adalah ideal. Selanjutnya diambil sebarang $a,b\in\left(N:M\right)$ dan $r\in R$ , maka akan berlaku hal-hal sebagai berikut:
1. Jelas $\left(N:M\right)\neq\emptyset$ karena $0\in\left(N:M\right)$ .
2. Karena $a,b\in\left(N:M\right)$ maka $aM\subseteq N$ dan $bM\subseteq N$ sehingga berlaku:

$\left(a-b\right)M=aM-bM\subseteq N$

Dengan kata lain, $a-b\in\left(N:M\right)$ .
3. Karena $aM\subseteq N$ maka untuk sebarang $r\in R$ berlaku:

$\left(ra\right)M=r\left(aM\right)\subseteq N$

Dengan kata lain, $ra\in\left(N:M\right)$ .
Dari tiga hal di atas, maka terbukti bahwa himpunan $\left(N:M\right)=\left\{ r\in R|rM\subseteq N\right\}$ adalah ideal di ring R.
Semoga tulisan pendek ini bermanfaat ya. Mari kita senantiasa berbagi ilmu pengetahuan, apa saja. Nuwun.

Saya yakin sudah familiar dengan bilangan Fibonacci atau disebut juga deret fibonacci. Suatu pola bilangan yang sederhana pada matematika tetapi ajaibnya pola tersebut banyak muncul di alam. Semua berawal dari 0 dan 1 lalu bilangan berikutnya merupakan hasil penhumlahan 2 bilangan sebelumnya

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

Bagaimana kita mencari bilangan ke-1000? atau ke-505? Untuk mencari bilangan ke-n dari bilangan fibonacci kita menggunakan rumus binet. Rumus tersebut berkata.

$F_{n}=\frac{1}{\sqrt{5}}\left(\left(\frac{1+\sqrt{5}}{2}\right)^{n}-\left(\frac{1-\sqrt{5}}{2}\right)^{n}\right)$

Ada beberapa cara untuk membuktikan rumus tersebut, dengan rekursif, dengan induksi dll. Sahabat saya Hendry Dext telah menuliskan pembuktian rumus binet. Saya juga mau membuktikan rumus binet tetapi dengan metode yang berbeda dengan Hendry. Saya akan menggunakan aljabar linier.
Pertama-tama kita akan membentuk sistem persamaan linier dengan 2 persamaan. Kita tahu bahwa suku ke n+2 fibonacci merupakan penjumlahan dari suku ke n+1 dan suku ke n. Kita peroleh persamaan yang pertama $F_{n+2}=F_{n+1}+F_{n}$ . Selanjutnya kita butu persamaan ke-2, cukup persamaan sederhana $F_{n+1}=F_{n+1}+0$ . Kita peroleh sistem persamaan linier

$F_{n+2}=F_{n+1}+F_{n}$

$F_{n+1}=F_{n+1}+0$

Jika sistem persamaandiatas diubah ke dalam persamaan matriks, diperoleh

$\left[\begin{array}{c}F_{n+2}\\F_{n+1}\end{array}\right]=\left[\begin{array}{cc}1 & 1\\1 & 0\end{array}\right]\left[\begin{array}{c}F_{n+1}\\F_{n}\end{array}\right]$

Oya sebelumnya notasi $F_n$ merupakan suku ke-n dari fibonacci dengan $F_0=0$ dan $F_1=1$ .

Jika kita notasikan $U_{n+1}=\left[{F_{n+2}\atop F_{n+1}}\right]$ , $A=\left[\begin{array}{cc}1 & 1\\1 & 0\end{array}\right]$ dan $U_{n}=\left[{F_{n+1}\atop F_{n}}\right]$ . Kita peroleh aturan dalam fibonacci

$U_{n+1}=AU_{n}$

Nah sekarang mari kita mulai menghitung

Jadi diperoleh rumus umum

$u_n=A^nu_0$

$\left[{F_{n+1}\atop F_{n}}\right]=A^{n}\left[{1\atop 0}\right]$

Nah..sekarang pertanyaannya adalah bagaimana menghitung pangkat ke-n dari matriks $A$ secara cepat?

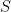
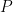
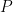
Cara cepatnya adalah dengan menggunakan 2 matriks spesial $S$ dan $P$ . Matriks $P$ adalah matriks diagonal yang memuat nilai-nilai eigen dari matriks $A$

$P=\left[\begin{array}{cc}\lambda_{1} & 0\\ 0 & \lambda_{2}\end{array}\right]$

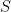
Sedangkan matriks $S$ adalah matriks yang kolom-kolomnya merupakan vektor-vektor eigen dari $A$ .
$S=\left[v_{1}\, v_{2}\right]$
diperoleh
$A=SPS^{-1}$
Berdasarkan persamaan diatas, dengan mudah kita dapet menghitung $A^2$
$A^2=SPS^{-1}SPS^{-1}$
$A^2=SPIPS^{-1}$
$A^2=SP^2S^{-1}$
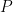
Karena $P$ merupakan matriks diagonal maka $P^2=\left[\begin{array}{cc}\lambda_{1}^2 & 0\\ 0 & \lambda_{2}^2\end{array}\right]$
Dengan cara sama kita mendapatkan $A^3=SP^3S^{-1}$ , dengan $P^3=\left[\begin{array}{cc}\lambda_{1}^3 & 0\\ 0 & \lambda_{2}^3\end{array}\right]$
Jadi dapat disimpulkan bahwa rumus mencari pangkat ke-n dari matriks $A$ adalah
$A^n=SP^nS^{-1}$
Nah sekarang berapa vektor eigen dan nilai eigen dari $A$ . Saya tidak akan melakukan perhitungan disini. Nilai egin dari $A$ adalah $\lambda_{1}=\frac{1+\sqrt{5}}{2}$ dan $\lambda_{1}=\frac{1-\sqrt{5}}{2}$ . Sedangkan vektor eigennya adalah $v_{1}=\left[{\lambda_{1}\atop 1}\right]$ dan $v_{2}=\left[{\lambda_{2}\atop 1}\right]$ . Silahkan kalain cek sendiri $Av_1=\lambda_{1}v_1$ dan $Av_2=\lambda_{1}v_2$ .
Kita peroleh
$S=\left[\begin{array}{cc}\lambda_{1} & \lambda_{2}\\1 & 1\end{array}\right]$
dan
$S^{-1}=\frac{1}{\lambda_{1}-\lambda_{2}}\left[\begin{array}{cc}1 & -\lambda_{2}\\-1 & \lambda_{1}\end{array}\right]$
Itu berarti kita peroleh
$u_n=A^nu_0$ .
$u_n=SP^nS^{-1}\left[{1\atop 0}\right]$
$u_{n}=SP^{n}\frac{1}{\lambda_{1}-\lambda_{2}}\left[{1\atop -1}\right]$
$u_{n}=S\frac{1}{\lambda_{1}-\lambda_{2}}\left[{\lambda_{1}^{n}\atop -\lambda_{2}^{n}}\right]$
$u_{n}=\frac{1}{\lambda_{1}-\lambda_{2}}\left[{\lambda_{1}^{n+1}-\lambda_{2}^{n+1}\atop \lambda_{1}^{n}-\lambda_{2}^{n}}\right]$
$\left[{F_{n+1}\atop F_{n}}\right]=\frac{1}{\lambda_{1}-\lambda_{2}}\left[{\lambda_{1}^{n+1}-\lambda_{2}^{n+1}\atop \lambda_{1}^{n}-\lambda_{2}^{n}}\right]$
Catetan: $\lambda_{1}-\lambda_{2}=\sqrt{5}$
Akhirnya kita dapat

$F_{n+1}=\frac{1}{\sqrt{5}}\left(\lambda_{1}^{n+1}-\lambda_{2}^{n+1}\right)$

$F_{n}=\frac{1}{\sqrt{5}}\left(\lambda_{1}^{n}-\lambda_{2}^{n}\right)$

Viola we got burnet’s formula

In your mind

Selasa, 07 Desember 2010

Lemma 2.3.4

Deret Fibonacci